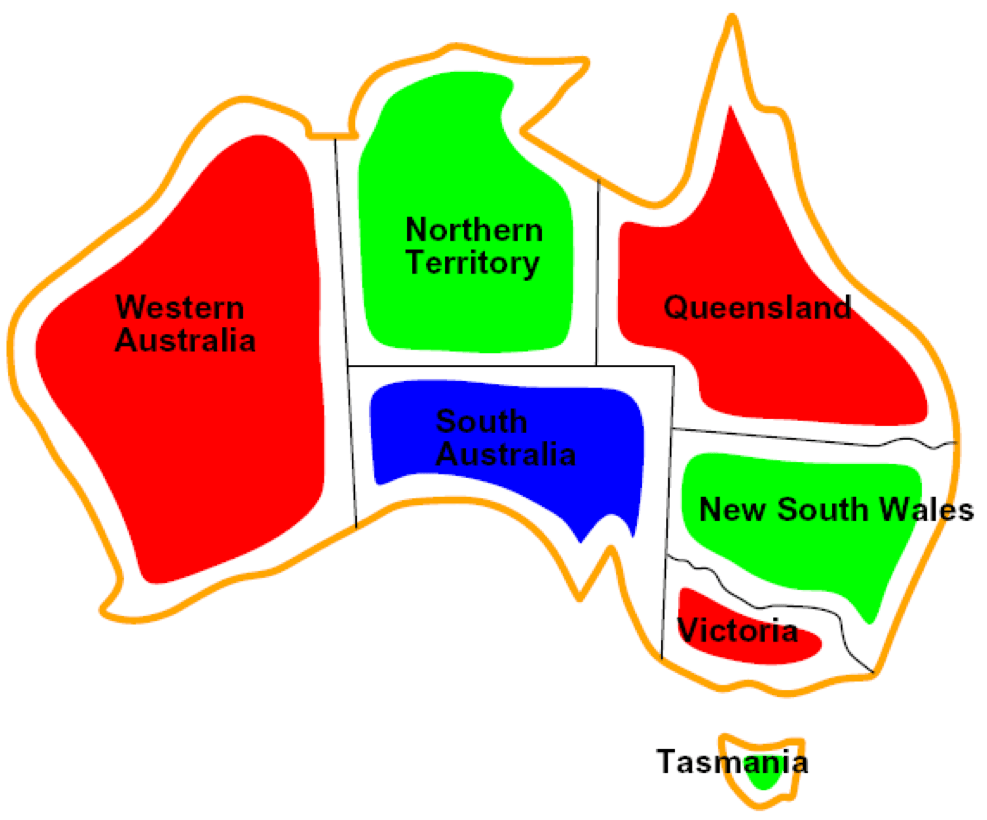
Graph Coloring Constraint Satisfaction Problem - In this problem, the color of nodes in a graph (map) are the variables, the set of available colors for each node. Map coloring is a classic problem in computer science and mathematics, particularly in the realm of graph theory and constraint. Graph coloring • consider n nodes in a graph • assign values v1,., vn to each of the n nodes • the values are taken in { r,g,b}. The goal is to assign colors to each region so that no neighboring. Add forward checking to the. In this blog post, we will see how to formulate csp problems using three basic components: Coloring this map can be viewed as a constraint satisfaction problem (csp). The tree_csp_solver function (figure 6.11 in the book) can be used to solve problems whose constraint graph is a tree. Add variable and value ordering to the implementation. Implement the following graph coloring algorithms:
Constraint Satisfaction I
Graph coloring • consider n nodes in a graph • assign values v1,., vn to each of the n nodes • the values are taken in { r,g,b}. In this problem, the color of nodes in a graph (map) are the variables, the set of available colors for each node. Add variable and value ordering to the implementation. Add forward.
Mapcoloring as constraint graph. One possible solution to the CSP is... Download Scientific
Graph coloring • consider n nodes in a graph • assign values v1,., vn to each of the n nodes • the values are taken in { r,g,b}. We use the map coloring problem to demonstrate the csp. The goal is to assign colors to each region so that no neighboring. Add variable and value ordering to the implementation. The.
Constraint Satisfaction Problems Map coloring and other examples of CSP YouTube
Add variable and value ordering to the implementation. We use the map coloring problem to demonstrate the csp. In this blog post, we will see how to formulate csp problems using three basic components: Map coloring is a classic problem in computer science and mathematics, particularly in the realm of graph theory and constraint. Implement the following graph coloring algorithms:
PPT Constraint Satisfaction Problems PowerPoint Presentation, free download ID584040
Map coloring is a classic problem in computer science and mathematics, particularly in the realm of graph theory and constraint. We use the map coloring problem to demonstrate the csp. Add forward checking to the. In this blog post, we will see how to formulate csp problems using three basic components: The tree_csp_solver function (figure 6.11 in the book) can.
Constraint Satisfaction Problem (CSP) Cryptarithmetic, Graph Coloring, 4 Queen, Sudoku PPT
Graph coloring • consider n nodes in a graph • assign values v1,., vn to each of the n nodes • the values are taken in { r,g,b}. Implement the following graph coloring algorithms: Add variable and value ordering to the implementation. Add forward checking to the. In this problem, the color of nodes in a graph (map) are the.
GitHub rohitsingh186/graphcoloringconstraintsatisfactionproblem `Graph Coloring Problem
Coloring this map can be viewed as a constraint satisfaction problem (csp). The goal is to assign colors to each region so that no neighboring. We use the map coloring problem to demonstrate the csp. Add variable and value ordering to the implementation. Graph coloring • consider n nodes in a graph • assign values v1,., vn to each of.
Constraint Satisfaction Problem (CSP) Cryptarithmetic, Graph Coloring, 4 Queen, Sudoku PPT
In this blog post, we will see how to formulate csp problems using three basic components: Add forward checking to the. Implement the following graph coloring algorithms: In this problem, the color of nodes in a graph (map) are the variables, the set of available colors for each node. The goal is to assign colors to each region so that.
Constraint Satisfaction Problem (CSP) Cryptarithmetic, Graph Coloring, 4 Queen, Sudoku PPT
In this problem, the color of nodes in a graph (map) are the variables, the set of available colors for each node. The goal is to assign colors to each region so that no neighboring. Map coloring is a classic problem in computer science and mathematics, particularly in the realm of graph theory and constraint. We use the map coloring.
Constraint Satisfaction Problem (CSP) Cryptarithmetic, Graph Coloring, 4 Queen, Sudoku PPT
The goal is to assign colors to each region so that no neighboring. The tree_csp_solver function (figure 6.11 in the book) can be used to solve problems whose constraint graph is a tree. Graph coloring • consider n nodes in a graph • assign values v1,., vn to each of the n nodes • the values are taken in {.
Constraint satisfaction problems ppt download
We use the map coloring problem to demonstrate the csp. Add variable and value ordering to the implementation. Coloring this map can be viewed as a constraint satisfaction problem (csp). Add forward checking to the. Implement the following graph coloring algorithms:
Add forward checking to the. Coloring this map can be viewed as a constraint satisfaction problem (csp). In this problem, the color of nodes in a graph (map) are the variables, the set of available colors for each node. We use the map coloring problem to demonstrate the csp. The tree_csp_solver function (figure 6.11 in the book) can be used to solve problems whose constraint graph is a tree. In this blog post, we will see how to formulate csp problems using three basic components: Add variable and value ordering to the implementation. Graph coloring • consider n nodes in a graph • assign values v1,., vn to each of the n nodes • the values are taken in { r,g,b}. Implement the following graph coloring algorithms: Map coloring is a classic problem in computer science and mathematics, particularly in the realm of graph theory and constraint. The goal is to assign colors to each region so that no neighboring.
The Tree_Csp_Solver Function (Figure 6.11 In The Book) Can Be Used To Solve Problems Whose Constraint Graph Is A Tree.
We use the map coloring problem to demonstrate the csp. Map coloring is a classic problem in computer science and mathematics, particularly in the realm of graph theory and constraint. In this blog post, we will see how to formulate csp problems using three basic components: In this problem, the color of nodes in a graph (map) are the variables, the set of available colors for each node.
Graph Coloring • Consider N Nodes In A Graph • Assign Values V1,., Vn To Each Of The N Nodes • The Values Are Taken In { R,G,B}.
Coloring this map can be viewed as a constraint satisfaction problem (csp). The goal is to assign colors to each region so that no neighboring. Add variable and value ordering to the implementation. Add forward checking to the.